19 Graphs, Networks, and Trees

內容

Graphical representations are widely used for displaying relations among informational units because they help readers to visualize those relations and hence to understand them better. Two general types of graphical representations may be distinguished.

Graphs, in the strictly mathematical sense, consist of points, often called nodes or vertices, and connections among them, called arcs, or under certain conditions, edges. Among the various types of graphs are networks and trees. Graphs generally and networks in particular are dealt with directly below. Trees are dealt with separately in sections 19.2 Trees and 19.3 Another Tree Notation. ⁷²
Charts, which typically plot data in two or more dimensions, including plots with orthogonal or radial axes, bar charts, pie charts, and the like. These can be described using the elements defined in the module for figures and graphics; see chapter 14 Tables, Formulæ, and Graphics.

Among the types of qualitative relations often represented by graphs are organizational hierarchies, flow charts, genealogies, semantic networks, transition networks, grammatical relations, tournament schedules, seating plans, and directions to people's houses. In developing recommendations for the encoding of graphs of various types, we have relied on their formal mathematical definitions and on the most common conventions for representing them visually. However, it must be emphasized that these recommendations do not provide for the full range of possible graphical representations, and deal only partially with questions of design, layout, and placement.

» 19.2 Trees
首頁 | 內容

19.1 Graphs and DigraphsTEI: Graphs and Digraphs¶

Broadly speaking, graphs can be divided into two types: undirected and directed. An undirected graph is a set of nodes (or vertices) together with a set of pairs of those vertices, called arcs or edges. Each node in an arc of an undirected graph is said to be incident with that arc, and the two vertices (nodes) which make up an arc are said to be adjacent. An directed graph is like an undirected graph except that the arcs are ordered pairs of nodes. In the case of directed graphs, the term edge is not used; moreover, each arc in a directed graph is said to be adjacent from the node from which the arc emanates, and adjacent to the node to which the arc is directed. We use the element graph to encode graphs as a whole, node to encode nodes or vertices, and arc to encode arcs or edges; arcs can also be encoded by attributes on the node element. These elements have the following descriptions and attributes:

graph 標記一個圖形，內含節點與節點之間的連線。
node 標記一個節點，一個圖形中可能帶有標籤的點。
arc 標記一條弧線，即為圖形中節點與節點之間的連線。

Before proceeding, some additional terminology may be helpful. We define a path in a graph as a sequence of nodes n1, ..., nk such that there is an arc from each ni to ni+1 in the sequence. A cyclic path, or cycle is a path leading from a particular node back to itself. A graph that contains at least one cycle is said to be cyclic; otherwise it is acyclic. We say, finally, that a graph is connected if there is a path from some node to every other node in the graph; any graph that is not connected is said to be disconnected.

Here is an example of an undirected, cyclic disconnected graph, in which the nodes are annotated with three-letter codes for airports, and the arcs connecting the nodes are represented by horizontal and vertical lines, with 90 degree bends used simply to avoid having to draw diagonal lines.

Next is a markup of the graph, using arc elements to encode the arcs.

<graph
  type="undirected"
  xml:id="CUG1"
  order="5"
  size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX" degree="2">
  <label>LAX</label>
</node>
<node xml:id="LVG" degree="2">
  <label>LVG</label>
</node>
<node xml:id="PHX" degree="3">
  <label>PHX</label>
</node>
<node xml:id="TUS" degree="1">
  <label>TUS</label>
</node>
<node xml:id="CIB" degree="0">
  <label>CIB</label>
</node>
<arc from="#LAX" to="#LVG"/>
<arc from="#LAX" to="#PHX"/>
<arc from="#LVG" to="#PHX"/>
<arc from="#PHX" to="#TUS"/>
</graph>

The first child element of graph may be a label to record a label for the graph; similarly, the label child of each node element records the labels of that node. The order and size attributes on the graph element record the number of nodes and number of arcs in the graph respectively; these values are optional (since they can be computed from the rest of the graph), but if they are supplied, they must be consistent with the rest of the encoding. They can thus be used to help check that the graph has been encoded and transmitted correctly. The degree attribute on the node elements record the number of arcs that are incident with that node. It is optional (because redundant), but can be used to help in validity checking: if a value is given, it must be consistent with the rest of the information in the graph. Finally, the from and to attributes on the arc elements provide pointers to the nodes connected by those arcs. Since the graph is undirected, no directionality is implied by the use of the from and to attributes; the values of these attributes could be interchanged in each arc without changing the graph.

The adj, adjFrom, and adjTo attributes of the node element provide an alternative method of representing unlabeled arcs, their values being pointers to the nodes which are adjacent to or from that node. The adj attribute is to be used for undirected graphs, and the adjFrom and adjTo attributes for directed graphs. It is a semantic error for the directed adjacency attributes to be used in an undirected graph, and vice versa. Here is a markup of the preceding graph, using the adj attribute to represent the arcs.

<graph
  type="undirected"
  xml:id="CUG2"
  order="5"
  size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX2" degree="2" adj="#LVG2 #PHX2">
  <label>LAX2</label>
</node>
<node xml:id="LVG2" degree="2" adj="#LAX2 #PHX2">
  <label>LVG2</label>
</node>
<node xml:id="PHX2" degree="3" adj="#LAX2 #LVG2 #TUS2">
  <label>PHX2</label>
</node>
<node xml:id="TUS2" degree="1" adj="#PHX2">
  <label>TUS2</label>
</node>
<node xml:id="CIB2" degree="0">
  <label>CIB2</label>
</node>
</graph>

Note that each arc is represented twice in this encoding of the graph. For example, the existence of the arc from LAX to LVG can be inferred from each of the first two node elements in the graph. This redundancy, however, is not required: it suffices to describe an arc in any one of the three places it can be described (either adjacent node, or in a separate arc element). Here is a less redundant representation of the same graph.

<graph
  type="undirected"
  xml:id="CUG3"
  order="5"
  size="4">
<label>Airline Connections in Southwestern USA</label>
<node xml:id="LAX3" degree="2" adj="#LVG3 #PHX3">
  <label>LAX3</label>
</node>
<node xml:id="LVG3" degree="2" adj="#PHX3">
  <label>LVG3</label>
</node>
<node xml:id="PHX3" degree="3" adj="#TUS3">
  <label>PHX3</label>
</node>
<node xml:id="TUS3" degree="1">
  <label>TUS3</label>
</node>
<node xml:id="CIB3" degree="0">
  <label>CIB3</label>
</node>
</graph>

Although in many cases the arc element is redundant (since arcs can be described using the adjacency attributes of their adjacent nodes), it has nevertheless been included in this module, in order to allow the convenient specification of identifiers, display or rendition information, and labels for each arc (using the attributes xml:id, rend, and a child label element).

Next, let us modify the preceding graph by adding directionality to the arcs. Specifically, we now think of the arcs as specifying selected routes from one airport to another, as indicated by the direction of the arrowheads in the following diagram.

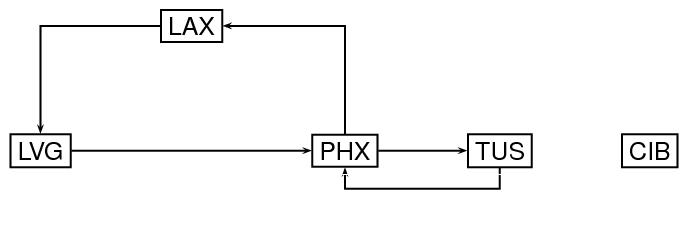
Here is an encoding of this graph, using the arc element to designate the arcs.

<graph
  type="directed"
  xml:id="RDG1"
  order="5"
  size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node xml:id="LAX4" inDegree="1" outDegree="1">
  <label>LAX4</label>
</node>
<node xml:id="LVG4" inDegree="1" outDegree="1">
  <label>LVG4</label>
</node>
<node xml:id="PHX4" inDegree="2" outDegree="2">
  <label>PHX4</label>
</node>
<node xml:id="TUS4" inDegree="1" outDegree="1">
  <label>TUS4</label>
</node>
<node xml:id="CIB4" inDegree="0" outDegree="0">
  <label>CIB4</label>
</node>
<arc from="#LAX4" to="#LVG4"/>
<arc from="#LVG4" to="#PHX4"/>
<arc from="#PHX4" to="#LAX4"/>
<arc from="#PHX4" to="#TUS4"/>
<arc from="#TUS4" to="#PHX4"/>
</graph>

The attributes inDegree and outDegree indicate the number of nodes which are adjacent to and from the node concerned respectively.

Here is another encoding of the graph, using the adjTo and adjFrom attributes on nodes to designate the arcs.

<graph
  type="directed"
  xml:id="RDG2"
  order="5"
  size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node
   xml:id="LAX5"
   inDegree="1"
   outDegree="1"
   adjTo="#LVG5"
   adjFrom="#PHX5">
  <label>LAX5</label>
</node>
<node
   xml:id="LVG5"
   inDegree="1"
   outDegree="1"
   adjFrom="#LAX5"
   adjTo="#PHX5">
  <label>LVG5</label>
</node>
<node
   xml:id="PHX5"
   inDegree="2"
   outDegree="2"
   adjTo="#LAX5 #TUS"
   adjFrom="#LVG5 #TUS5">
  <label>PHX5</label>
</node>
<node
   xml:id="TUS5"
   inDegree="1"
   outDegree="1"
   adjTo="#PHX5"
   adjFrom="#PHX5">
  <label>TUS5</label>
</node>
<node xml:id="CIB5" inDegree="0" outDegree="0">
  <label>CIB5</label>
</node>
</graph>

If we wish to label the arcs, say with flight numbers, then arc elements must be used to hold the label elements, as in the following example.

<graph
  type="directed"
  xml:id="RDG3"
  order="5"
  size="5">
<label>Selected Airline Routes in Southwestern USA</label>
<node xml:id="LAX6">
  <label>LAX6</label>
</node>
<node xml:id="LVG6">
  <label>LVG6</label>
</node>
<node xml:id="PHX6">
  <label>PHX6</label>
</node>
<node xml:id="TUS6">
  <label>TUS6</label>
</node>
<node xml:id="CIB6">
  <label>CIB6</label>
</node>
<arc from="#LAX6" to="#LVG6">
  <label>SW117</label>
</arc>
<arc from="#LVG6" to="#PHX6">
  <label>SW711</label>
</arc>
<arc from="#PHX6" to="#LAX6">
  <label>AA218</label>
</arc>
<arc from="#PHX6" to="#TUS6">
  <label>AW229</label>
</arc>
<arc from="#TUS6" to="#PHX6">
  <label>AW225</label>
</arc>
</graph>

» 19.1.2 Family Trees
首頁 | 內容

19.1.1 Transition NetworksTEI: Transition Networks¶

For encoding transition networks and other kinds of directed graphs in which distinctions among types of nodes must be made, the type attribute is provided for node elements. In the following example, the initial and final nodes (or states) of the network are distinguished. It can be understood as accepting the set of strings obtained by traversing it from its initial node to its final node, and concatenating the labels.

<graph
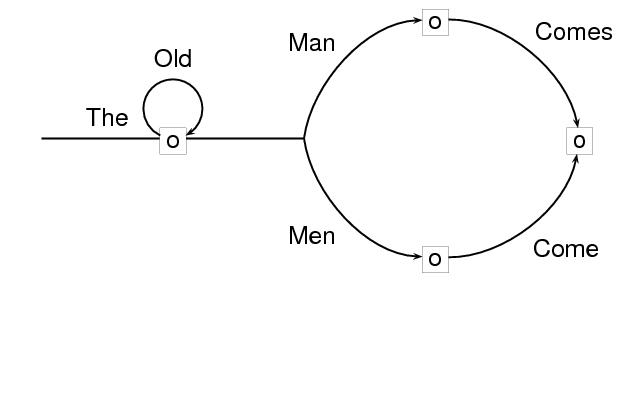
  type="network-transition"
  xml:id="SS8"
  order="5"
  size="6">
<label>(8)</label>
<node
   xml:id="Q0"
   inDegree="0"
   outDegree="1"
   type="initial"/>
<node xml:id="Q1" inDegree="2" outDegree="3"/>
<node xml:id="Q2" inDegree="1" outDegree="1"/>
<node xml:id="Q3" inDegree="1" outDegree="1"/>
<node
   xml:id="Q4"
   inDegree="2"
   outDegree="0"
   type="final"/>
<arc from="#Q0" to="#Q1">
  <label>THE</label>
</arc>
<arc from="#Q1" to="#Q1">
  <label>OLD</label>
</arc>
<arc from="#Q1" to="#Q2">
  <label>MAN</label>
</arc>
<arc from="#Q1" to="#Q3">
  <label>MEN</label>
</arc>
<arc from="#Q2" to="#Q4">
  <label>COMES</label>
</arc>
<arc from="#Q3" to="#Q4">
  <label>COME</label>
</arc>
</graph>

A finite state transducer has two labels on each arc, and can be thought of as representing a mapping from one sequence of labels to the other. The following example represents a transducer for translating the English strings accepted by the network in the preceding example into French. The nodes have been annotated with numbers, for convenience.

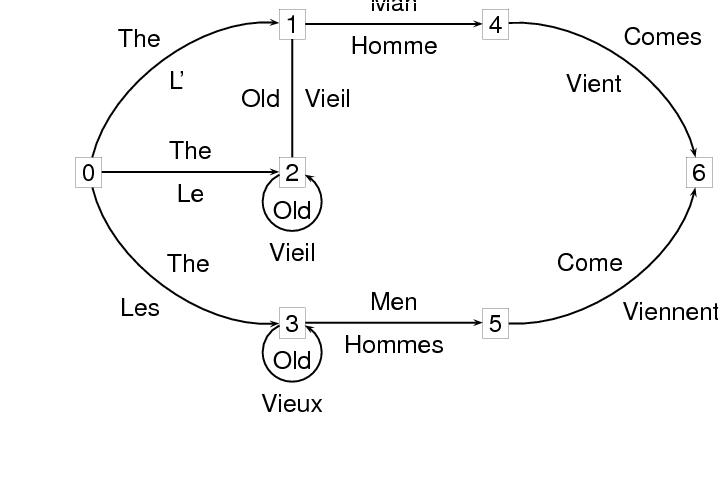
<graph type="transducer" order="7" size="10">
<node
   xml:id="T0"
   inDegree="0"
   outDegree="3"
   type="initial">
  <label>0</label>
</node>
<node xml:id="T1" inDegree="2" outDegree="1">
  <label>1</label>
</node>
<node xml:id="T2" inDegree="2" outDegree="2">
  <label>2</label>
</node>
<node xml:id="T3" inDegree="2" outDegree="2">
  <label>3</label>
</node>
<node xml:id="T4" inDegree="1" outDegree="1">
  <label>4</label>
</node>
<node xml:id="T5" inDegree="1" outDegree="1">
  <label>5</label>
</node>
<node
   xml:id="T6"
   inDegree="2"
   outDegree="0"
   type="final">
  <label>6</label>
</node>
<arc from="#T0" to="#T1">
  <label>THE</label>
  <label>L'</label>
</arc>
<arc from="#T0" to="#T2">
  <label>THE</label>
  <label>LE</label>
</arc>
<arc from="#T0" to="#T3">
  <label>THE</label>
  <label>LES</label>
</arc>
<arc from="#T1" to="#T4">
  <label>MAN</label>
  <label>HOMME</label>
</arc>
<arc from="#T2" to="#T1">
  <label>OLD</label>
  <label>VIEIL</label>
</arc>
<arc from="#T2" to="#T2">
  <label>OLD</label>
  <label>VIEIL</label>
</arc>
<arc from="#T3" to="#T3">
  <label>OLD</label>
  <label>VIEUX</label>
</arc>
<arc from="#T3" to="#T5">
  <label>MEN</label>
  <label>HOMMES</label>
</arc>
<arc from="#T4" to="#T6">
  <label>COMES</label>
  <label>VIENT</label>
</arc>
<arc from="#T5" to="#T6">
  <label>COME</label>
  <label>VIENNENT</label>
</arc>
</graph>

19.1.2 Family TreesTEI: Family Trees¶

The next example provides an encoding a portion of a family tree, in which nodes are used to represent individuals and parents of individuals, and arcs are used to represent common parentage and descent links. Let us suppose, further, that information about individuals is contained in feature structures, which are contained in feature-structure libraries elsewhere (see 18.4 Feature and Feature-Value Libraries). We can use the value attribute on node elements to point to those feature structures. In this particular representation of the graph, nodes representing females are framed by ovals, nodes representing males are framed by boxes, and nodes representing parents are framed by diamonds.

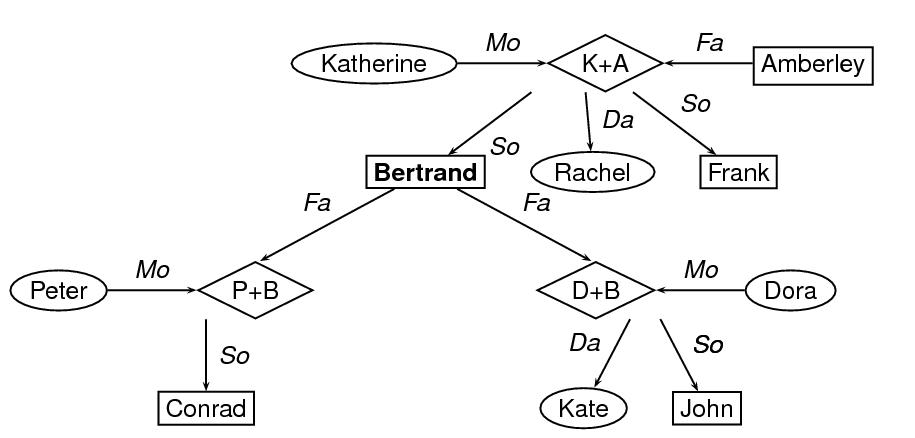
<graph type="family_tree" order="13" size="12">
<node
   xml:id="KATHR"
   value="http://example.com/russell-fs/tei/kr1"
   inDegree="0"
   outDegree="1">
  <label>Katherine</label>
</node>
<node
   xml:id="AMBER"
   value="http://example.com/russell-fs/tei/ar1"
   inDegree="0"
   outDegree="1">
  <label>Amberley</label>
</node>
<node xml:id="KAR" inDegree="2" outDegree="3">
  <label>K+A</label>
</node>
<node
   xml:id="BERTR"
   value="http://example.com/russell-fs/tei/br1"
   inDegree="1"
   outDegree="2">
  <label>Bertrand</label>
</node>
<node
   xml:id="PETER"
   value="http://example.com/russell-fs/tei/pr1"
   inDegree="0"
   outDegree="1">
  <label>Peter</label>
</node>
<node
   xml:id="DORAR"
   value="http://example.com/russell-fs/tei/dr1"
   inDegree="0"
   outDegree="1">
  <label>Dora</label>
</node>
<node xml:id="PBR" inDegree="2" outDegree="1">
  <label>P+B</label>
</node>
<node xml:id="DBR" inDegree="2" outDegree="2">
  <label>D+B</label>
</node>
<node
   xml:id="FRANR"
   value="http://example.com/russell-fs/tei/fr1"
   inDegree="1"
   outDegree="0">
  <label>Frank</label>
</node>
<node
   xml:id="RACHR"
   value="http://example.com/russell-fs/tei/rr1"
   inDegree="1"
   outDegree="0">
  <label>Rachel</label>
</node>
<node
   xml:id="CONRR"
   value="http://example.com/russell-fs/tei/cr1"
   inDegree="1"
   outDegree="0">
  <label>Conrad</label>
</node>
<node
   xml:id="KATER"
   value="http://example.com/russell-fs/tei/kr2"
   inDegree="1"
   outDegree="0">
  <label>Kate</label>
</node>
<node
   xml:id="JOHNR"
   value="http://example.com/russell-fs/tei/jr1"
   inDegree="1"
   outDegree="0">
  <label>John</label>
</node>
<arc from="#KATHR" to="#KAR">
  <label>Mo</label>
</arc>
<arc from="#AMBER" to="#KAR">
  <label>Fa</label>
</arc>
<arc from="#KAR" to="#BERTR">
  <label>So</label>
</arc>
<arc from="#KAR" to="#FRANR">
  <label>So</label>
</arc>
<arc from="#KAR" to="#RACHR">
  <label>Da</label>
</arc>
<arc from="#PETER" to="#PBR">
  <label>Mo</label>
</arc>
<arc from="#BERTR" to="#PBR">
  <label>Fa</label>
</arc>
<arc from="#PBR" to="#CONRR">
  <label>So</label>
</arc>
<arc from="#DORAR" to="#DBR">
  <label>Mo</label>
</arc>
<arc from="#BERTR" to="#DBR">
  <label>Fa</label>
</arc>
<arc from="#DBR" to="#KATER">
  <label>Da</label>
</arc>
<arc from="#DBR" to="#JOHNR">
  <label>So</label>
</arc>
</graph>

bibliography

« 19.1.2 Family Trees
首頁 | 內容

19.1.3 Historical InterpretationTEI: Historical Interpretation¶

For our final example, we represent graphically the relationships among various geographic areas mentioned in a seventeenth-century Scottish document. The document itself is a ‘sasine’, which records a grant of land from the earl of Argyll to one Donald McNeill, and reads in part as follows (abbreviations have been expanded silently, and ‘[...]’ marks illegible passages):

Item instrument of Sasine given the said Hector Mcneil confirmed and dated 28 May 1632 [...] at Edinburgh upon the 15 June 1632

Item ane charter granted by Archibald late earl of Argyle and Donald McNeill of Gallachalzie wh makes mention that ... the said late Earl yields and grants to the said Donald MacNeill ...

All and hail the two merk land of old extent of Gallachalzie with the pertinents by and in the lordship of Knapdale within the sherrifdome of Argyll

[description of other lands granted follows ...]

This Charter is dated at Inverary the 15th May 1669

In this example, we are concerned with the land and pertinents (i.e. accompanying sources of revenue) described as ‘the two merk land of old extent of Gallachalzie with the pertinents by and in the lordship of Knapdale within the sherrifdom of Argyll’.

The passage concerns the following pieces of land:

the Earl of Argyll's land (i.e. the lands granted by this clause of the sasine)
two mark of land in Gallachalzie
the pertinents for this land
the Lordship of Knapdale
the sherrifdom of Argyll

We will represent these geographic entities as nodes in a graph. Arcs in the graph will represent the following relationships among them:

containment (INCLUDE)
location within (IN)
contiguity (BY)
constituency (PART OF)

Note that these relationships are logically related: ‘include’ and ‘in’, for example, are inverses of each other: the Earl of Argyll's land includes the parcel in Gallachalzie, and the parcel is therefore in the Earl of Argyll's land. Given an explicit set of inference rules, an appropriate application could use the graph we are constructing to infer the logical consequences of the relationships we identify.

Let us assume that feature-structure analyses are available which describe Gallachalzie, Knapdale, and Argyll. We will link to those feature structures using the value attribute on the nodes representing those places. However, there may be some uncertainty as to which noun phrase is modified by the phrase ‘within the sheriffdome of Argyll’: perhaps the entire lands (land and pertinents) are in Argyll, perhaps just the pertinents are, or perhaps only Knapdale is (together with the portion of the pertinents which is in Knapdale). We will represent all three of these interpretations in the graph; they are, however, mutually exclusive, which we represent using the exclude attribute defined in chapter 16 Linking, Segmentation, and Alignment. ⁷³

We represent the graph and its encoding as follows, where the dotted lines in the graph indicate the mutually exclusive arcs; in the encoding, we use the exclude attribute to indicate those arcs.

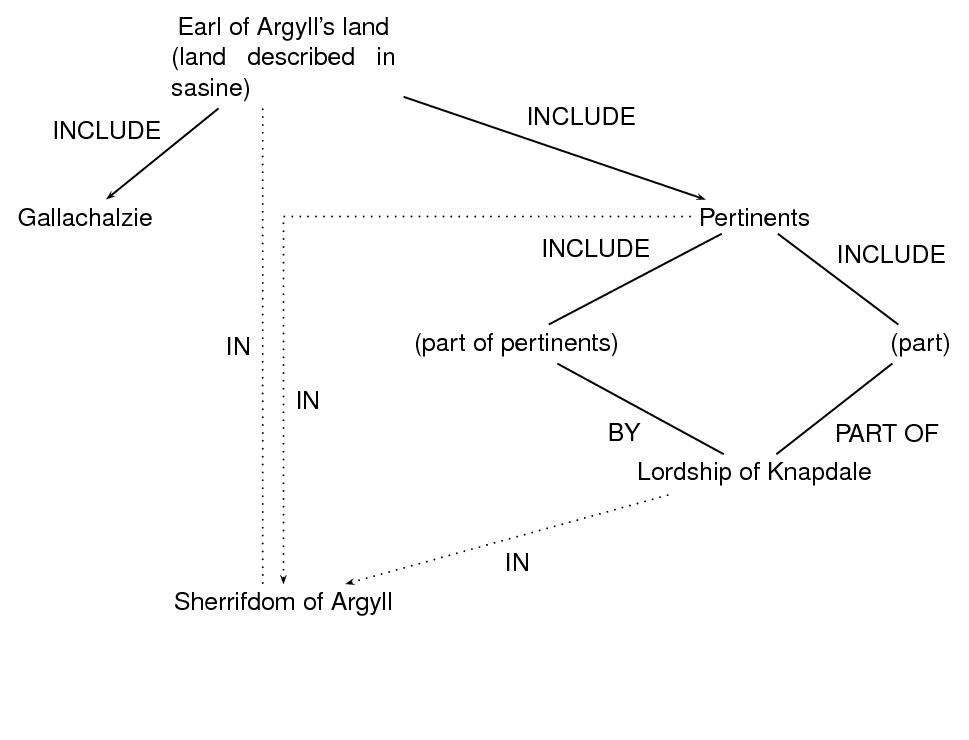
The graph formalizes the following relationships:

the Earl of Argyll's land includes (the parcel of land in) Gallachalzie
the Earl of Argyll's land includes the pertinents of that parcel
the pertinents are (in part) by the Lordship of Knapdale
the pertinents are (in part) part of the Lordship of Knapdale
the Earl of Argyll's land, or the pertinents, or the Lordship of Knapdale, is in the Sherrifdom of Argyll

We encode the graph thus:

<graph type="directed" order="7" size="9">
<node xml:id="EARL">
  <label>Earl of Argyll's land</label>
</node>
<node xml:id="GALL"
   value="http://example.com/people/scots#gall">
  <label>Gallachalzie</label>
</node>
<node xml:id="PERT">
  <label>Pertinents</label>
</node>
<node xml:id="PER1">
  <label>Pertinents part</label>
</node>
<node xml:id="PER2">
  <label>Pertinents part</label>
</node>
<node
   xml:id="KNAP"
   value="http://example.com/people/scots#knapfs">
  <label>Lordship of Knapdale</label>
</node>
<node
   xml:id="ARGY"
   value="http://example.com/people/scots#argyfs">
  <label>Sherrifdome of Argyll</label>
</node>
<arc xml:id="EARLGALL" from="#EARL" to="#GALL">
  <label>INCLUDE</label>
</arc>
<arc
   xml:id="EARLARGY"
   from="#EARL"
   to="#ARGY"
   exclude="#PERTARGY #KNAPARGY">
  <label>IN</label>
</arc>
<arc xml:id="EARLPERT" from="#EARL" to="#PERT">
  <label>INCLUDE</label>
</arc>
<arc xml:id="PERTPER1" from="#PERT" to="#PER1">
  <label>INCLUDE</label>
</arc>
<arc xml:id="PERTPER2" from="#PERT" to="#PER2">
  <label>INCLUDE</label>
</arc>
<arc
   xml:id="PERTARGY"
   from="#PERT"
   to="#ARGY"
   exclude="#EARLARGY #KNAPARGY">
  <label>IN</label>
</arc>
<arc xml:id="PER1KNAP" from="#PER1" to="#KNAP">
  <label>BY</label>
</arc>
<arc xml:id="PER2KNAP" from="#PER2" to="#KNAP">
  <label>PART OF</label>
</arc>
<arc
   xml:id="KNAPARGY"
   from="#KNAP"
   to="#ARGY"
   exclude="#EARLARGY #PERTARGY">
  <label>IN</label>
</arc>
</graph>

19.2 TreesTEI: Trees¶

A tree is a connected acyclic graph. That is, it is possible in a tree graph to follow a path from any vertex to any other vertex, but there are no paths that lead from any vertex to itself. A rooted tree is a directed graph based on a tree; that is, the arcs in the graph correspond to the arcs of a tree such that there is exactly one node, called the root, for which there is a path from that node to all other nodes in the graph. For our purposes, we may ignore all trees except for rooted trees, and hence we shall use the tree element for rooted trees, and the root element for its root. The nodes adjacent to a given node are called its children, and the node adjacent from a given node is called its parent. Nodes with both a parent and children are called internal nodes, for which we use the iNode element. A node with no children is tagged as a leaf. If the children of a node are ordered from left to right, then we say that that node is ordered. If all the nodes of a tree are ordered, then we say that the tree is an ordered tree. If some of the nodes of a tree are ordered and others are not, then the tree is a partially ordered tree. The ordering of nodes and trees may be specified by an attribute; we take the default ordering for trees to be ordered, that roots inherit their ordering from the trees in which they occur, and internal nodes inherit their ordering from their parents. Finally, we permit a node to be specified as following other nodes, which (when its parent is ordered) it would be assumed to precede, giving rise to crossing arcs. The elements used for the encoding of trees have the following descriptions and attributes.

tree 標記一個樹狀結構，包含根節點、內部節點、葉節點、以及從根到葉的連線。

arity	根節點所擁有的子節點數以及樹狀結構的內部節點數的最大值。
ord	(ordered) 說明樹狀結構是否整齊排列，或是部分整齊排列。
order	提供樹狀結構的次序，例如節點數目。

root (根節點) 樹狀結構的根節點。

value	提供一個根節點值，該跟節點為一個功能結構或其他分析元素。
children	提供根節點的子節點元素識別符碼列表。
ord	(ordered) 說明根節點是否整齊排列。
outDegree	根節點的向外分支度，即為其子節點的數量。

iNode (中間 (或內部) 節點) 表示一個樹狀結構的中間 (或內部) 節點。

value	提供一個中間節點值，該節點為一個功能結構或其他分析元素。
children	提供中間節點的子節點之元素識別符碼列表。
parent	提供中間節點的雙親節點的元素識別符碼。
ord	(ordered) 說明內部節點是否整齊排列。
follow	提供此節點所尾隨的元素識別符碼。
outDegree	中間節點的向外分支度，即為其子節點的數量。

leaf 標記樹狀結構的葉節點 (終端節點) 。

value	提供一個連結到功能結構或其他分析元素的指標。
parent	提供葉節點的父節點識別符碼。
follow	提供此葉節點所尾隨的元素識別符碼。

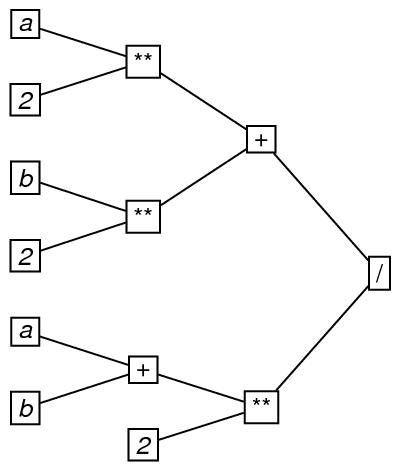
Here is an example of a tree. It represents the order in which the operators of addition (symbolized by +), exponentiation (symbolized by **) and division (symbolized by /) are applied in evaluating the arithmetic formula ((a**2)+(b**2))/((a+b)**2). In drawing the graph, the root is placed on the far right, and directionality is presumed to be to the left.

In this encoding, the arity attribute represents the arity of the tree, which is the greatest value of the outDegree attribute for any of the nodes in the tree. If, as in this case, arity is 2, we say that the tree is a binary tree.

Since the left-to-right (or top-to-bottom!) order of the children of the two + nodes does not affect the arithmetic result in this case, we could represent in this tree all of the arithmetically equivalent formulas involving its leaves, by specifying the attribute ord as false on those two iNode elements, the attribute ord as true on the root and other iNode elements, and the attribute ord as partial on the tree element, as follows.

This encoding represents all of the following:

((a**2)+(b**2))/((a+b)**2)
((b**2)+(a**2))/((a+b)**2)
((a**2)+(b**2))/((b+a)**2)
((b**2)+(a**2))/((a+b)**2)

Linguistic phrase structure is very commonly represented by trees. Here is an example of phrase structure represented by an ordered tree with its root at the top, and a possible encoding.

<tree
  n="ex3"
  ord="true"
  arity="2"
  order="8">
<root xml:id="GD-PP1" children="#GD-P1 #GD-NP1">
  <label>PP</label>
</root>
<iNode xml:id="GD-P1" parent="#GD-PP1" children="#GD-WITH1">
  <label>P</label>
</iNode>
<leaf xml:id="GD-WITH1" parent="#GD-P1">
  <label>with</label>
</leaf>
<iNode xml:id="GD-NP1" parent="#GD-PP1" children="#GD-THE1 #GD-PERI1">
  <label>NP</label>
</iNode>
<iNode xml:id="GD-ART1" parent="#GD-NP1" children="#GD-THE1">
  <label>Art</label>
</iNode>
<leaf xml:id="GD-THE1" parent="#GD-ART1">
  <label>the</label>
</leaf>
<iNode xml:id="GD-N1" parent="#GD-NP1" children="#GD-PERI1">
  <label>N</label>
</iNode>
<leaf xml:id="GD-PERI1" parent="#GD-N1">
  <label>periscope</label>
</leaf>
</tree>

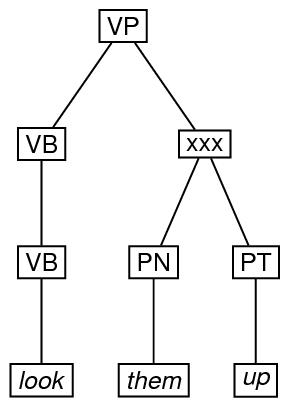
Finally, here is an example of an ordered tree, in which a particular node which ordinarily would precede another is specified as following it. In the drawing, the xxx symbol indicates that the arc from VB to PT crosses the arc from VP to PN.

« 19.2 Trees
» 19.4 Representing Textual Transmission
首頁 | 內容

19.3 Another Tree NotationTEI: Another Tree Notation¶

In this section, we present an alternative to the method of representing the structure of ordered rooted trees given in section 19.2 Trees, which is based on the observation that any node of such a tree can be thought of as the root of the subtree that it dominates. Thus subtrees can be thought of as the same type as the trees they are embedded in, hence the designation eTree, for embedding tree. Whereas in a tree the relationship among the parts is indicated by the children attribute, and by the names of the elements root, iNode, and leaf, the relationship among the parts of an eTree is indicated simply by the arrangement of their content. However, we have chosen to enable encoders to distinguish the terminal elements of an eTree by means of the empty eLeaf element, though its use is not required; the eTree element can also be used to identify the terminal nodes of eTree elements. We also provide a triangle element, which can be thought of as an underspecified eTree, i.e. an eTree in which certain information has been left out. In addition, we provide a forest element, which consists of one or more tree, eTree, or triangle elements, and a forestGrp element, which consists of one or more forest elements. The elements used for the encoding of embedding trees and the units containing them have the following descriptions and attributes.

eTree (嵌入樹狀結構) 提供樹元素的替換，用來表示整齊具有根節點的樹狀結構。

value

提供一個嵌入樹狀結構值，該嵌入樹狀結構為一個功能結構或其他分析元素。

triangle (不完全嵌入樹狀結構，如同畫出的圖形特徵所顯示。) 為不完全之<嵌入樹狀結構>所提供的元素，即資訊不足的<嵌入樹狀結構>。

value

提供一個三角樹狀結構值，該三角樹狀結構為一個功能結構或其他分析元素。

eLeaf (嵌入樹狀結構的葉節點。) 為嵌入樹狀結構的葉節點所明確提供的元素，也可用元素eTree來標記。

value

提供一個嵌入葉節點值，該嵌入葉節點為一個功能結構或其他分析元素。

forest 匯集具根節點的樹狀結構群組。

type 標明森林的類型。
forestGrp (森林群組) 匯集森林群組。

type 標明森林群組的類型。

Like the root, iNode, and leaf of a tree, the eTree, triangle and eLeaf elements may also have value attributes and label children.

To illustrate the use of the eTree and eLeaf elements, here is an encoding of the second example in section 19.2 Trees, repeated here for convenience.

<eTree n="ex1">
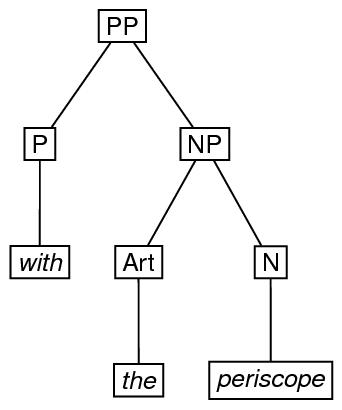
<label>PP</label>
<eTree>
  <label>P</label>
  <eLeaf>
   <label>with</label>
  </eLeaf>
</eTree>
<eTree>
  <label>NP</label>
  <eTree>
   <label>Art</label>
   <eLeaf>
    <label>the</label>
   </eLeaf>
  </eTree>
  <eTree>
   <label>N</label>
   <eLeaf>
    <label>periscope</label>
   </eLeaf>
  </eTree>
</eTree>
</eTree>

Next, we provide an encoding, using the triangle element, in which the internal structure of the eTree labeled NP is omitted.

<eTree n="ex2">
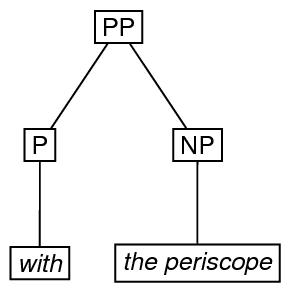
<label>PP</label>
<eTree>
  <label>P</label>
  <eLeaf>
   <label>with</label>
  </eLeaf>
</eTree>
<triangle>
  <label>NP</label>
  <eLeaf>
   <label>the periscope</label>
  </eLeaf>
</triangle>
</eTree>

Ambiguity involving alternative tree structures associated with the same terminal sequence can be encoded relatively conveniently using a combination of the exclude and copyOf attributes described in sections 16.8 Alternation and 16.6 Identical Elements and Virtual Copies. In the simplest case, an eTree may be part of the content of exactly one of two different eTree elements. To mark it up, the embedded eTree may be fully specified within one of the embedding eTree elements to which it may belong, and a virtual copy, specified by the copyOf attribute, may appear on the other. In addition, each of the embedded elements in question is specified as excluding the other, using the exclude attribute. To illustrate, consider the English phrase see the vessel with the periscope, which may be considered to be structurally ambiguous, depending on whether the phrase with the periscope is a modifier of the phrase the vessel or a modifier of the phrase see the vessel. This ambiguity is indicated in the sketch of the ambiguous tree by means of the dotted-line arcs. The markup using the copyOf and exclude attributes follows the sketch.

<eTree n="ex3">
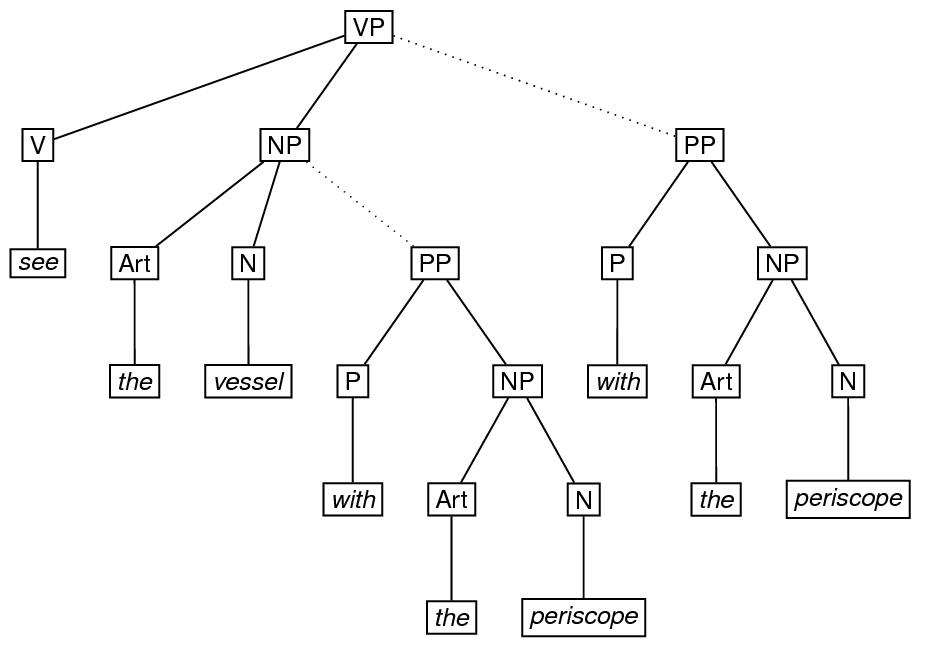
<label>VP</label>
<eTree>
  <label>V</label>
  <eLeaf>
   <label>see</label>
  </eLeaf>
</eTree>
<eTree>
  <label>NP</label>
  <eTree>
   <label>Art</label>
   <eLeaf>
    <label>the</label>
   </eLeaf>
  </eTree>
  <eTree>
   <label>N</label>
   <eLeaf>
    <label>vessel</label>
   </eLeaf>
  </eTree>
  <eTree xml:id="GD-PPA" exclude="#GD-PPB">
   <label>PP</label>
   <eTree>
    <label>P</label>
    <eLeaf>
     <label>with</label>
    </eLeaf>
   </eTree>
   <eTree>
    <label>NP</label>
    <eTree>
     <label>Art</label>
     <eLeaf>
      <label>the</label>
     </eLeaf>
    </eTree>
    <eTree>
     <label>N</label>
     <eLeaf>
      <label>periscope</label>
     </eLeaf>
    </eTree>
   </eTree>
  </eTree>
</eTree>
<eTree xml:id="GD-PPB" copyOf="#GD-PPA" exclude="#GD-PPA">
  <label>PP</label>
</eTree>
</eTree>

To indicate that one of the alternatives is selected, one may specify the select attribute on the highest eTree as either #GD-PPA or #GD-PPB; see section 16.8 Alternation.

Depending on the grammar one uses to associate structures with examples like see the man with the periscope, the representations may be more complicated than this. For example, adopting a version of the X-bar theory of phrase structure originated by Jackendoff, ⁷⁴ the attachment of a modifier may require the creation of an intermediate node which is not required when the attachment is not made, as shown in the following diagram. A possible encoding of this ambiguous structure immediately follows the diagram.

<eTree n="ex4">
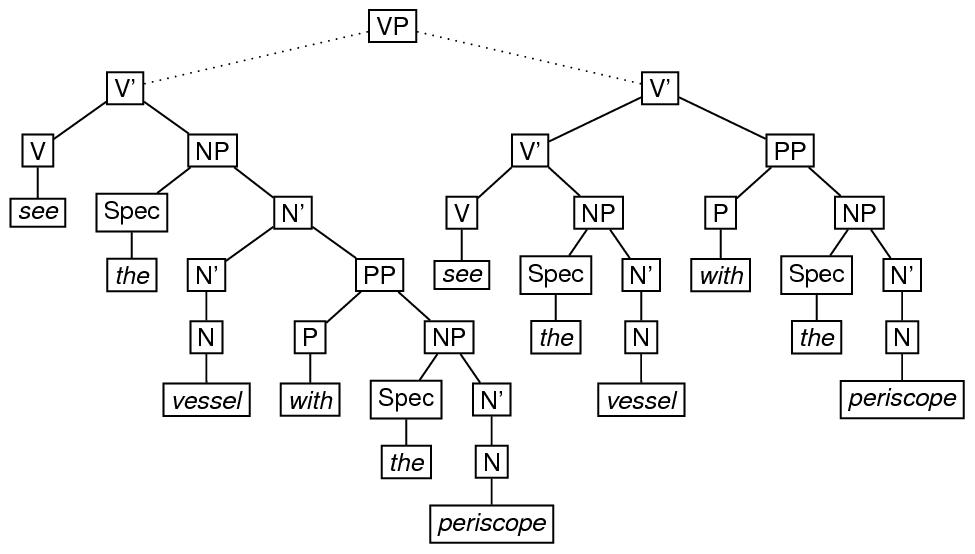
<label>VP</label>
<eTree xml:id="VBARA" exclude="#VBARB">
  <label>V'</label>
  <eTree xml:id="VA">
   <label>V</label>
   <eLeaf>
    <label>see</label>
   </eLeaf>
  </eTree>
  <eTree>
   <label>NP</label>
   <eTree xml:id="SPEC1A">
    <label>Spec</label>
    <eLeaf>
     <label>the</label>
    </eLeaf>
   </eTree>
   <eTree>
    <label>N'</label>
    <eTree xml:id="NBAR2A">
     <label>N'</label>
     <eTree>
      <label>N</label>
      <eLeaf>
       <label>vessel</label>
      </eLeaf>
     </eTree>
    </eTree>
    <eTree xml:id="PPA1">
     <label>PP</label>
     <eTree>
      <label>P</label>
      <eLeaf>
       <label>with</label>
      </eLeaf>
     </eTree>
     <eTree>
      <label>NP</label>
      <eTree>
       <label>Spec</label>
       <eLeaf>
        <label>the</label>
       </eLeaf>
      </eTree>
      <eTree>
       <label>N'</label>
       <eTree>
        <label>N</label>
        <eLeaf>
         <label>periscope</label>
        </eLeaf>
       </eTree>
      </eTree>
     </eTree>
    </eTree>
   </eTree>
  </eTree>
</eTree>
<eTree xml:id="VBARB" exclude="#VBARA">
  <label>V'</label>
  <eTree>
   <label>V'</label>
   <eTree xml:id="VB" copyOf="#VA">
    <label>V</label>
   </eTree>
   <eTree>
    <label>NP</label>
    <eTree xml:id="SPEC1B" copyOf="#SPEC1A">
     <label>Spec</label>
    </eTree>
    <eTree xml:id="NBAR2B" copyOf="#NBAR2A">
     <label>N'</label>
    </eTree>
   </eTree>
  </eTree>
  <eTree xml:id="PPB" copyOf="#PPA1">
   <label>PP</label>
  </eTree>
</eTree>
</eTree>

A derivation in a generative grammar is often thought of as a set of trees. To encode such a derivation, one may use the forest element, in which the trees may be marked up using the tree, the eTree, or the triangle element. The type attribute may be used to specify what kind of derivation it is. Here is an example of a two-tree forest, involving application of the ‘wh-movement’ transformation in the derivation of what you do (as in this is what you do) from the underlying you do what. ⁷⁵

In this markup, we have used copyOf attributes to provide virtual copies of elements in the tree representing the second stage of the derivation that also occur in the first stage, and the corresp attribute (see section 16.4 Correspondence and Alignment) to link those elements in the second stage with corresponding elements in the first stage that are not copies of them.

If a group of forests (e.g. a full grammatical derivation including syntactic, semantic, and phonological subderivations) is to be articulated, the grouping element forestGrp may be used.

19.4 Representing Textual TransmissionTEI: Representing Textual Transmission¶

A stemma codicum (sometimes called just stemma) is a tree-like graphic structure that has become traditional in manuscript studies for representing textual transmission. Consider the following hypothetical stemma:

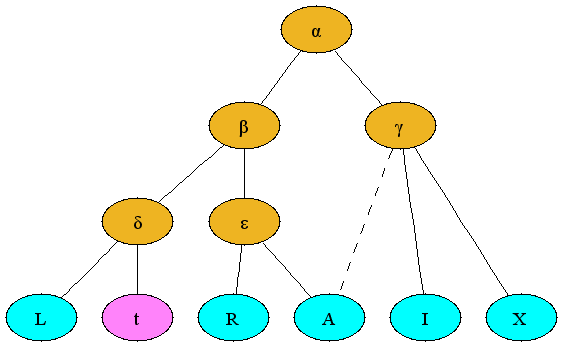
圖表 4. Example stemma

The nodes in this stemma represent manuscripts; each has a label (a letter) which identifies it and also distinguishes whether the manuscript is extant, lost, or hypothetical. Extant manuscripts are identified by uppercase Latin letters or words beginning with uppercase Latin letters, e.g., L, shown as aqua in this example; manuscripts no longer existing, but providing readings which are attested e.g. by note or copy made before their disappearance, are identified by lowercase Latin letters, e.g., t, shown as magenta in this example; hypothetical stages in the textual transmission, which do not necessarily correspond to real manuscripts, are given lowercase Greek letters, e.g., α and shown as gold in this example. The stemma shown above thus suggests that (on the basis of similarities in the readings of the extant and lost manuscripts) L and t share textual material that is not shared with other manuscripts (represented in this case by δ) even though no physical manuscript attesting this stage in the textual transmission has ever been identified.

Manuscripts are copied from other manuscripts. The preceding stemma represents the hypothesis that all manuscripts go back to a common ancestor (α), that the tradition split after that stage into two (β and γ), etc. Descent by copying is indicated with a solid line. According to this model, α is the earliest common hypothetical stage that can be reconstructed, and all nodes below α have a single parent, that is, were copied from a single other stage in the tradition.

This familiar tree model is complicated because manuscripts sometimes show the influence of more than one ancestor. They may have been produced by a scribe who checked the text in one manuscript of the same work whilst copying from another, or perhaps made changes from his memory of a slightly different version of the text that he had read elsewhere. Alternatively, perhaps scribe A copied a manuscript from one source, scribe B made changes in it in the margins or between the lines (either by consulting another source directly or from memory), and another scribe then copied that manuscript, incorporating the changes into the body. Whatever the specific scenario, it is not uncommon for a manuscript to be based primarily on one source, but to incorporate features of another branch of the tradition. This mixed result is called contamination, and it is reflected in a stemma by a dotted line. Thus, the example above asserts that A is copied within the ε tradition, but is also contaminated from the γ tradition.

The utility of a stemma as a visualization tool is inversely proportional to the degree of contamination in the manuscript tradition. A tradition completely without contamination (called a closed tradition) yields a classic tree, easily represented graphically by a stemma. An open tradition, with substantial contamination, yields a spaghetti-like stemma characterized by crossing dotted lines, which is both difficult to read and not very informative.

The eTree element introduced in this chapter can be used to represent a closed tradition in a straightforward manner. Each non-terminal node is represented by a typed eTree element and each terminal node by an eLeaf. A label element provides a way of identifying each node, complementary to the global attributes n and xml:id attributes. For example, the closed part of the tradition headed by the label δ may be encoded as follows:

To complete this representation, we need to show that the node labelled A is not derived solely from its parent node (labelled ε) but also demonstrates contamination from the node labelled γ. The easiest way to accomplish this is to include an appropriately-typed ptr element within the node in question, the target of which points to the node labelled γ. This requires that this latter node be supplied with a value for its xml:id attribute. The complete representation is thus:

In any substantial codicological project, it is likely that significantly more data will be required about the individual witnesses than indicated in the simple structures above. These Guidelines provide a rich variety of additional elements for representing such information: see in particular chapters 10 Manuscript Description, 11 Representation of Primary Sources, and 12 Critical Apparatus.

19.5 Module for Graphs, Networks, and TreesTEI: Module for Graphs, Networks, and Trees¶

The module described in this chapter makes available the following components:

組件 nets: 圖形、網絡與樹狀結構

被定義的元素: arc eLeaf eTree forest forestGrp graph iNode leaf node root tree triangle

The selection and combination of modules to form a TEI schema is described in 1.2 Defining a TEI Schema.

↑ 內容 « 18 Feature Structures » 20 Non-hierarchical Structures

註解

72.

The treatment here is largely based on the characterizations of graph types in Chartrand and Lesniak (1986)

↵

73.

That is, the three syntactic interpretations of the clause are mutually exclusive. The notion that the pertinents are in Argyll is clearly not inconsistent with the notion that both the land in Gallachalzie and the pertinents are in Argyll. The graph given here describes the possible interpretations of the clause itself, not the sets of inferences derivable from each syntactic interpretation, for which it would be convenient to use the facilities described in chapter 18 Feature Structures.

↵

74.

Jackendoff (1977)

↵

75.

The symbols e and t denote special theoretical constructs (empty category and trace respectively), which need not concern us here.

↵

[English] [Deutsch] [Español] [Italiano] [Français] [日本語] [한국어] [中文]

Copyright TEI Consortium 2007 Licensed under the GPL. Copying and redistribution is permitted and encouraged.
Version 1.7.0. Last updated on July 6th 2010.This page generated on 2010-07-07T22:07:32Z

P5: TEI指引